| Main index | Electoral System index | About author |
Julian D. A. Wiseman
Abstract: PR-Squared gives mid-size parties a strong incentive to merge. PR-Squared gives voters a strong incentive to avoid small parties. This paper explores these majoritarian incentives.
Publication history: Only at www.jdawiseman.com/papers/electsys/pr2_vote_power_party_merge.html. Usual disclaimer and copyright terms apply.
Contents: Introduction (Assumed Size of 120); The Parties’ Incentive (Compatible Policies); The Voters’ Incentive; Conclusion; Footnotes.
PR-Squared is a new electoral system. It was originally designed for the UK’s House of Commons, but would work well in other countries, particularly those seeking to increase the majoritarian-ness of a vanilla electoral PR system. PR-Squared typically elects a majority government; it elects one MP from each constituency each of whom is dependent on the local vote; yet it still ensures that equal votes mean equal seats.
PR-Squared works as follows (the various technicalities being discussed in PR-Squared: A New Description):
The country is divided into single-member constituencies;
In each constituency each party may field at most one candidate;
Voters cast a single vote in favour of a single candidate;
The votes for each party are totalled nation-wide;
The key rule: each party is allocated seats in proportion to the square of its nation-wide vote;
As only a whole number of seats can be won, the seat allocations must be rounded, which is done using the method of major fractions (also known as the method of odd numbers, Webster’s method, and the method of Saint-Lagüe).
It is now known how many seats each party has won, but not which constituencies. Constituencies are allocated to the parties in the manner that maximises the nation-wide total of the number of voters who voted for their local MP. Equivalently, define a ‘happy voter’ to be a voter who voted for his or her MP, and then assign seat winners so as to maximise the nation’s total ‘happiness’.
For the purposes of this exposition, the crucial quality is the squaring. The squaring gives voters an incentive to vote for non-small parties. The squaring gives parties an incentive to form formal coalitions before an election—coalitions therefore visible to voters—rather than in post-election negotiations. This essay examines the range and strengths of these incentives, starting with that on parties.
In order to be concrete, throughout this essay it is assumed that 120 MPs are to be elected, this being the size of New Zealand’s House of Representatives, of the Israeli Knesset, and also of the Assembly of the Republic of Macedonia. So readers considering the merits of PR-Squared for the UK’s House of Commons should multiply by about 5½, and for Italy’s Chamber of Deputies by 5¼.
Consider the position of two parties, X and Y, with policies sufficiently similar that a post-election coalition is likely. Standing alone, these two parties are likely to gain unrounded seat totals of x and y. How many seats, out of 120, would be gained by merging before the election, rather than after?
This question is answered by the next chart, which repays some study.
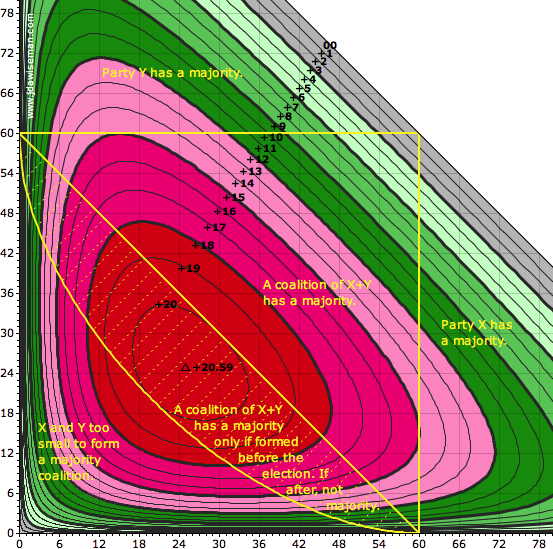 |
So given the number of seats each of two parties would win standing alone, x and y, the contours show the number of seats gained by merging before rather than after: that is, the reward from the squaring. This gain rises from zero (if either party would win zero seats, or if the two parties share all the seats), up to a peak of just over +20½ seats, achieved when each party standing alone would win almost 25 seats†1.
In particular, coloured red is the zone showing which mergers gain ≥18 seats: roughly, this covers mergers between parties with 12 to 45 seats, 10% to 37½% of the house. It is these small- to mid-size parties which have the strongest incentive to merge.
Superimposed on the seat-gain contours and colours are yellow lines, dividing the area into five classes of result.
Party X might win over half the seats, giving it a majority with which it can govern alone. This might be caused by PR-Squared: X might be the result of previous mergers incentivised by the squaring.
Or party Y might win over half the seats, giving it a majority with which it can govern alone—Y perhaps being the result of previous mergers incentivised by the squaring.
Parties X and Y might be smaller than this, but still large enough to share a majority of the seats.
The yellow dashing highlights the purpose of the squaring: in this zone a coalition of X and Y wins a majority only if that coalition is formed before the election.†2 A coalition formed by post-election haggling would be too small; the coalition must be formed before, to benefit from the squaring. Such a coalition would have the desirable property of being visible to voters when they cast their votes.
Or X and Y might be too small to form a majority government, whether or not negotiating a coalition before the election.
As a specific example, assume that five parties (A, B, C, D, and E) split the vote in the proportions 109: 65: 65: 25: 13 (≈ 39.4%: 23.5%: 23.5%: 9.0%: 4.7%). Then the seats are awarded proportionate to the square of these: 56.2%: 20.0%: 20.0%: 3.0%: 0.8%. A has a substantial majority: 12% of the house, being 14 seats out of 120 (or in UK terms 82 out of 646). But if B and C had merged before the election, then B+C, having just under 47% of the vote, would win 57% of the house, a majority of 16 seats. If B and C have policies that are even slightly compatible, they have a very strong incentive to negotiate that coalition before the election.
Note also that coalitions cannot be purely tactical, to ‘game’ the squaring rule. Each party may field at most one candidate in each constituency—a merger means that many candidates would have to stand aside. And even post-merger the choice of which candidates are elected falls to the voters, not to authors of a party list. So mergers are compelled to have at least some substance.
Some sets of politicians have deeply incompatible policies. Taxes designed for economic efficiency, or “tax the rich until the pips squeak”? Peace through negotiation, or peace through total victory? Abortion: a woman’s right, or murder? If conflicting sets of politicians attempt to write a manifesto, the public might well deem it incoherent. This doesn’t deny that there are workable coalitions: indeed, most large parties are de facto coalitions of groups insisting on a few social or economic values, while accepting those of their bedfellows (including US Republican, US Democrat, UK Conservative, UK Labour). So what pairs of parties are really “compatible”?
Under PR-Squared there is a minimum standard of compatibility: that the union of the two parties receive at least as many seats as sum of the seats received separately. This depends on the relative sizes of the merging parties, and the proportion of the separate votes that would be retained by the coalition.†3 The following chart shows the proportion of the combined parties’ votes that must be retained to win at least as many seats, as a function of the ratio of the numbers of votes received by the two parties.
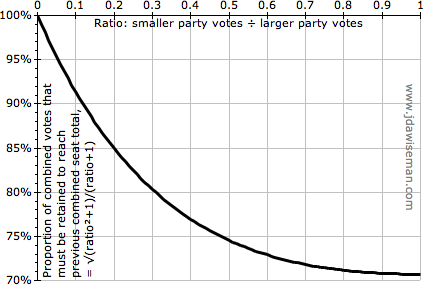 |
If two parties receive similar-ish numbers of votes, within a factor of ×/÷2, then retaining ≈75% or more of the combined parties’ votes, that would result in a gain in seats. For any pair of parties that would have been likely to form a post-election coalition, this standard is easily met: they gain by forming that coalition in advance, revealing it to the electorate.
But for small parties things are different. If a large party is merging with a tiny party, even a small loss of votes can penalise this: large parties should avoid small parties with taboo policies. And if two one-seat parties are merging, and hold their votes, the coalition gets about four seats. This isn’t much: two parties with no power have become one party with no power, and have paid a price of a loss of doctrinal purity (a typical one-seat party is not a ‘broad church’!). So the majoritarian incentive on small parties is weaker: but, as is about to be explained, the majoritarian incentive on small parties’ voters is very powerful.
How many extra votes are needed for an extra seat? This seemingly easy question is a little complicated.
Of course, this should speak of unrounded seats. It might happen to be that one extra vote would push a party’s unrounded seat total high enough that it would round up to the next seat. But if this were so, a second extra vote would be ‘worthless’—in the sense of not changing the rounded seats. So, as with the discussion above (The Parties’ Incentive), this discussion is about unrounded seats. But there are still three possible meanings to the question.
Single-seat: How many extra votes are required to gain one extra unrounded seat?
Single-vote: What part of an unrounded seat is gained by a single extra vote?
Continuous: What is (∂UnroundedSeats/∂Votes)–1?
Each of these three has different uses: parties care about single-seat, voters about single-vote, and if quoting votes or seats or both as a proportion of the total, then continuous is most useful, and it also has the advantage of greater mathematical tractability.
The following chart shows how these three vary for different sizes of party. It assumes that the votes for the other parties are fixed, the sum of their squares being 1366⅞bn (changing this number merely rescaling the y axis).
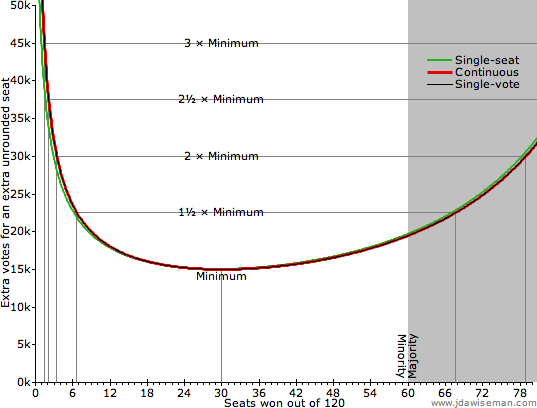 |
Happily, the three measures of ‘how many extra votes are needed for an extra seat?’ are very similar for parties larger than tiny. Votes are most powerful if given to parties winning a quarter of the seats.†4 And for parties winning anything from 5.5% to over half of the seats, votes have a power within a factor of 1½ of this. But tiny parties are punished hard. If a party would win 2.8% of the house, a vote is only half as powerful as for a party ten times larger. Voters’ effective choice is one ‘vote’ for this unpopular party, or two for a popular party? At least some voters would defect to the larger party, and, in doing so, would strengthen the incentive on the others.
Which parties are bitten by this incentive? Assume that the largest party has a modest majority, winning, say, 53% of the house. Then a party that wins 2.8% of the house has 0.052× as many seats, caused by winning √0.052 ≈ 0.23× as many votes. Once a party starts receiving less than a quarter of the largest party’s votes, it is in danger of withering away within an election or few. Depending on the number of parties and distribution of votes, this gives a de facto minimum size for parties of about 10% of the votes.
The power of a vote has another pleasing property. Using either the single-vote or continuous measures, any party other than the largest party needs fewer extra voters per extra seat than does any smaller party.†5 So if a voter wishes to evict the incumbent government—arguably the most important purpose of democracy—that is most effectively done by voting for the largest opposition party.
So PR-Squared gives strong majoritarian incentives to both voters and parties, but different incentives.
Votes are more powerful if given to non-tiny parties.
Parties of size from small to just-sub-majority would gain many seats by forming formal coalitions before the election.
And thus will voters choose a government—surely more democratic than voters merely vaguely influencing a post-election haggle for ministries and special favours.
Julian D. A. Wiseman, New York, 13th April 2009
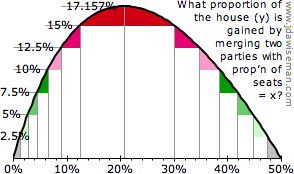 |
†1 The maximum gain, as a proportion of the house, is (3–2√2) ≈ 17.157%. This occurs when both parties, standing alone, would win ½(√2–1) ≈ 20.71% of the house, giving a combined total of (2–√2) ≈ 58.58%, the majority happening to equal the gain of (3–2√2). See chart on the right, being, and coloured as, the x = y diagonal of the above seat-gain chart.
†2 The curved boundary satisfies 4 (x2 + x y + y2) = TotalNumSeats (4x + 4y – TotalNumSeats), implying y = ½( TotalNumSeats – x – √[x (2 TotalNumSeats – 3x)] ). On this boundary the minimum value of x + y occurs when x = y = TotalNumSeats ÷ 6. If n parties were merging, the equivalent would be TotalNumSeats ÷ (n2 + n).
†3 If the two parties’ votes differ by a factor of r, then the proportion of votes that must be retained to break even is (√[r2+1])/(r+1). Observe that this is not changed by replacing r with r–1.
†4 Seatsi = Votesi2 / (Votesi2 + SumOtherVotesSquares). Thus, for a house of unit size, ∂2Seatsi/∂Votesi2 = 2×SumOtherVotesSquares×(SumOtherVotesSquares–3×Votesi2) / ((Votesi2+SumOtherVotesSquares)³). This solves to zero with SumOtherVotesSquares = 3×Votesi2, implying that party i won exactly one quarter of the seats. At this point the number of votes per extra seat is exactly (8/9)×√[3×SumOtherVotesSquares]. This is the minimum using the continuous measure. For single-vote the minimum lies about ½ a vote to the left of this; and for single-seat it lies about ½ a seat to the left of the continuous measure’s minimum.
†5 Hypothesis: using either the single-vote or continuous measures, any party other than the largest party needs fewer extra voters per extra seat than does any smaller party.
Proof: first using the continuous measure. We number parties 0, 1, 2, …, party i receiving vi votes, with v0 ≥ vi ≥ 0 ∀i, and v0 > 0. Choose non-zero integers p and q such that vp > vq. Let M = ∑vi2, and N = M – v02 – vp2 – vq2. Then the unrounded proportion of seats won by party i is Si = vi2 / M, and ∂Si/∂vi = 2 vi (M – vi2) / M2. So (∂Sp/∂vp)–1 < (∂Sq/∂vq)–1 ⇔ ∂Sp/∂vp > ∂Sq/∂vq ⇔ 2 vp (M – vp2) / M2 > 2 vq (M – vq2) / M2 ⇔ vp (M – vp2) > vq (M –vq2) ⇔ vp (N + v02 + vq2) > vq (N + v02 + vp2) ⇔ (vp – vq) (N + v02) > (vp – vq) vp vq ⇔ N + v02 > vp vq which is true as v0 ≥ vp > vq ≥ 0, and N ≥ 0. So, as required, a vote for the second-largest party is more powerful than a vote for the third largest, which in turn is powerful than a vote for the fourth, etc. But the position of the largest party is undefined. For example, if the votes split 2:1:1:1:1 then the largest party requires the least votes per extra ∂seat. If 3:2:1:1:1 then the largest party requires the second least; if 4:2:2:1:1 third; if 5:2:2:2:1 fourth; and if 4:1:1:1:1 the most additional votes.
Second, the single-vote measure, for which the algebra is more complicated, but the principle similar. Use the same definitions as in the continuous case, with v0 ≥ vi+1 ≥ 0 ∀i and vp ≥ vq+1. We need to show that ( (vp+1)2 / (M + 2 vp + 1) – (vp2 / M) )–1 < ( (vq+1)2 / (M + 2 vq + 1) – (vq2 / M) )–1 ⇔ (vp+1)2 / (M + 2 vp + 1) – (vp2 / M) > (vq+1)2 / (M + 2 vq + 1) – (vq2 / M). Bring everything to the left of the equation and multiply by M (M + 2 vp + 1) (M + 2 vq + 1) ÷ (vp – vq), each factor of which is positive. Then replace M with N + v02 + vp2 + vq2; replace v0 with vp + 1 + x; and replace vp with vq + 1 + y. Simplify (or ExpandAll[…]), resulting in a 45-term polynomial in N, x, y, and vq. Every term of this polynomial has a positive sign, and every parameter is positive, and the constant term is +32. So, as required, the inequality holds. But, again, the value of a vote to the largest party can be the biggest, smallest, or any position in between, as shown by the voting ratios 4:3:3:3:3, 5:3:1:1:1, 3:2:2:1:1, 4:3:1:1:1, and 2:1:1:1:1.
Third, the single-seat measure, for which the result does not quite hold. The number of extra votes required to have an additional unrounded seat is √[vi2 + (∑v2) / (TotalNumSeats×(1 – vi2/(∑v2)) – 1)] – vi, and this seems not to have the neat ordering property. For example, with three seats and votes split 3:2:1, the 1-vote party requires an extra ⅕√221 – 1 ≈ 1.97 votes to get one more unrounded seat, whereas the 2-vote party requires ½√65 – 2 ≈ 2.03 extra votes for another seat. However, single-seat seems not to be the wrong way round by very much, and only to be wrong at all when the the number of seats is small. For example, if the votes split 7:6:5:4, then with 3 seats the entire ordering is reversed from the usual pattern: a smaller party requires less extra votes to gain an extra unrounded seat. But if the number of seats ≥7 then the usual pattern resumes. And as PR-Squared is done at a national level, usually meaning ≥100 seats, this oddity is unimportant. Indeed, the author suspects that there may well be a simple function of vp ÷ vq, such that if the number of seats exceeds that function for all suitable p and q, then the property holds even with the single-seat measure. The author would welcome being sent such a function.
| Main index | Top | About author |