| Main index | Electoral System index | About author |
Julian D. A. Wiseman
Abstract: It is desired to allocate a fixed number of seats proportional to some numbers (such as votes, population or even votes squared). If each entity is to receive an integer number of seats, then the allocations must be rounded. There are several ways to do this, with interesting and surprising properties.
Contents: Publication History, Introduction, Largest Remainder, Webster, Jefferson, Quotient methods, d’Hondt, Saint-Laguë, Modified Saint-Laguë, Danish, Imperiali, Breaching quota, Other systems, Statistics, with 659 seats, PR-Squared
Publication history: only here. Usual disclaimer and copyright terms apply.
In many electoral systems seats are assigned proportionally: in PR-classic, in proportion to the votes; in PR-Squared, to the squares of the votes. For example, imagine that 11 seats are to be divided in the proportions 59:26:16:7. The ‘correct’ number of seats for each party would be 6.01, 2.65, 1.63 and 0.71. However, seats have to be whole numbers; how are these to be rounded? There are several different apportionment schemes, none of which are perfect. The main such schemes are described here, along with their features and flaws.
The ‘largest-remainder’ method, also known as the ‘Hamilton’ method, is perhaps the most intuitive. Start by calculating the ‘unrounded’ seats, also known as the quota. These are the 6.01, 2.65, 1.63 and 0.71 already cited. Round down. Each party receives at least that many seats: 6, 2, 1 and 0. Two seats remain to be allocated, and these two seats are allocated to the parties with the largest remainders, in this example the 0.65 and the 0.71, for a final seat allocation of 6, 3, 1, and 1. In summary:
Method |
Target proportions |
Seat total |
Quota |
Seats |
|||||||||
| Largest remainder | 59 | 26 | 16 | 7 | 11 | 6.009 | 2.648 | 1.630 | 0.713 | 6 | 3 | 1 | 1 |
So far, so fair. However, there is a problem. Consider allocating 4 seats in the ratio 5:3:1. The unrounded seats are 2.222, 1.333 and 0.444, for a preliminary allocation of 2:1:0. Only 1 seat remains to be allocated; the largest remainder is 0.444, for a final allocation 2:1:1. But what if, instead, there were 5 seats to be allocated? Unrounded seats of 2.777, 1.666, and 0.555, give a preliminary allocation of 2:1:0; the two largest remainders are 0.777 and 0.666, for a final score of 3:2:0.
Method |
Target proportions |
Seat total |
Quota |
Seats |
||||||
| Largest remainder |
5 | 3 | 1 | 4 | 2.222 | 1.333 | 0.444 | 2 | 1 | 1 |
| 5 | 2.777 | 1.666 | 0.555 | 3 | 2 | 0 | ||||
Compare 2:1:1 to 3:2:0! An increase in the total number of seats has caused the smallest party to lose a seat. Surely the same share of a larger pie shouldn’t be smaller?
In the US, each state sends a number of Representatives, the number being proportional to its population. After the 1880 census it was observed that a House size of 299 would allow Alabama 8 seats, but a size of 300 would reduce this to 7. Hence this feature of the largest-remainder method is known as the ‘Alabama Paradox’.
Indeed, largest remainder has another undesirable feature. Imagine that there are three ‘serious’ parties, genuine contenders for government, and that there is also a minor party, too small to win seats. To be specific, perhaps imagine that this minor party is the UK’s Official Monster Raving Loony Party: amusing, but not a government in waiting. In proportions 50:17:4:0 a total of 11 seats are to be allocated; giving unrounded totals of 7.75 : 2.63 : 0.62 : 0.00, and hence a seat allocation of 8:3:0:0. But what if the minor party had managed to rouse a small number of voters from their slumbers? The results, summarised in the following table, are surprising.
Method |
Target proportions |
Seat total |
Quota |
Seats |
|||||||||
| Largest remainder |
50 | 17 | 4 | 0 | 11 | 7.75 | 2.63 | 0.62 | 0.00 | 8 | 3 | 0 | 0 |
| 1 | 7.64 | 2.60 | 0.61 | 0.15 | 8 | 2 | 1 | 0 | |||||
| 2 | 7.53 | 2.56 | 0.60 | 0.30 | 7 | 3 | 1 | 0 | |||||
The tiny party does not win a seat in any of these scenarios. But nonetheless, its acquiring a small number of votes can affect the allocation of the seats between the non-tiny parties. Note that in the top row the third party is to be assigned 4/61 of the seats, and receives none, but in the second row is to receive a slightly smaller 4/62 of the seats, but receives 1.
The Webster method proceeds by finding a divisor, l. Start with the target proportions; divide each by l, and round to the nearest whole number. If l is too low, this will give too many seats. If l too high, too few. Of the values of l that give the correct number of seats, choose the largest. So, in the 59:26:16:7 example, choose l to be 32/3, which gives unrounded seats of 5.53125, 2.4375, 1.5, and 0.65625, which round to 6, 2, 2 and 1.
Method |
Target proportions |
Seat total |
l |
Unrounded |
Seats |
|||||||||
| L. R. | 59 | 26 | 16 | 7 | 11 | 6.009 | 2.648 | 1.630 | 0.713 | 6 | 3 | 1 | 1 | |
| Webster | 32/3 | 5.53125 | 2.4375 | 1.5 | 0.65625 | 6 | 2 | 2 | 1 | |||||
The Jefferson method is similar to the Webster method. Again, start with the target proportions; and again divide each by l, but rounding down instead of to the nearest. To compare this to the Webster method, let us take a minimal example, in which two parties are to split 3 seats in the ratio 4:1. The Webster divisor l would be 2, giving seats of 2 and 0.5 which round to 2 and 1. But Jefferson rounds down, so l must be smaller, in this case 4/3, giving seats of 3 and 0.75, which round to 3 and 0. In summary:
Method |
Target proportions |
Seat total |
l |
Unrounded |
Seats |
|||
| Webster | 4 | 1 | 3 | 2 | 2 | 0.5 | 2 | 1 |
| Jefferson | 4/3 | 3 | 0.75 | 3 | 0 | |||
This result is typical: Jefferson advantages large parties more than Webster, and disadvantages small parties, a pattern which can also be seen in the now-familiar 11-seat 59:26:16:7 example:
Method |
Target proportions |
Seat total |
l |
Unrounded |
Seats |
|||||||||
| Jefferson | 59 | 26 | 16 | 7 | 11 | 59/7 | 7 | 3.085 | 1.899 | 0.831 | 7 | 3 | 1 | 0 |
| L. R. | 6.009 | 2.648 | 1.630 | 0.713 | 6 | 3 | 1 | 1 | ||||||
| Webster | 32/3 | 5.53125 | 2.4375 | 1.5 | 0.65625 | 6 | 2 | 2 | 1 | |||||
Quotient methods perform the allocation one seat at a time. Start with the target proportions, and allocate the first seat to the party with the largest such proportion. This party now has a seat, and so its target proportion is divided by a divisor. What divisor?
The d’Hondt rule says that the divisors are simply one more than the number of seats that party already has. The table shows this process at work in the 59:26:16:7 example. The first seat goes to the largest party, and its 59-part share is then replaced by a 59/2 = 29.50 part share. It is still the largest party (the largest party is shown in bold), so gains the next seat, and its share replaced by 59/3 = 19.6666, which means that the third seat to be allocated goes to the second-largest party. The process is continued until all 11 seats are allocated.
| Quotients | Seats | ||||||
| 59 | 26 | 16 | 7 | 1 | 0 | 0 | 0 |
| 29.50 | 26 | 16 | 7 | 2 | 0 | 0 | 0 |
| 19.67 | 26 | 16 | 7 | 2 | 1 | 0 | 0 |
| 19.67 | 13 | 16 | 7 | 3 | 1 | 0 | 0 |
| 14.75 | 13 | 16 | 7 | 3 | 1 | 1 | 0 |
| 14.75 | 13 | 8 | 7 | 4 | 1 | 1 | 0 |
| 11.80 | 13 | 8 | 7 | 4 | 2 | 1 | 0 |
| 11.80 | 8.67 | 8 | 7 | 5 | 2 | 1 | 0 |
| 9.83 | 8.67 | 8 | 7 | 6 | 2 | 1 | 0 |
| 8.43 | 8.67 | 8 | 7 | 6 | 3 | 1 | 0 |
| 8.43 | 6.50 | 8 | 7 | 7 | 3 | 1 | 0 |
This example used the d’Hondt rule, with divisors 1, 2, 3, 4, 5, 6, etc. The d’Hondt rule always gives exactly the same allocation of seats as the Jefferson method.
The Saint-Laguë rule uses divisors 1, 3, 5, 7, 9, etc; this is equivalent to the Webster method:
| Quotients | Seats | ||||||
| 59 | 26 | 16 | 7 | 1 | 0 | 0 | 0 |
| 19.67 | 26 | 16 | 7 | 1 | 1 | 0 | 0 |
| 19.67 | 8.67 | 16 | 7 | 2 | 1 | 0 | 0 |
| 11.80 | 8.67 | 16 | 7 | 2 | 1 | 1 | 0 |
| 11.80 | 8.67 | 5.33 | 7 | 3 | 1 | 1 | 0 |
| 8.43 | 8.67 | 5.33 | 7 | 3 | 2 | 1 | 0 |
| 8.43 | 5.20 | 5.33 | 7 | 4 | 2 | 1 | 0 |
| 6.56 | 5.20 | 5.33 | 7 | 4 | 2 | 1 | 1 |
| 6.56 | 5.20 | 5.33 | 2.33 | 5 | 2 | 1 | 1 |
| 5.36 | 5.20 | 5.33 | 2.33 | 6 | 2 | 1 | 1 |
| 4.54 | 5.20 | 5.33 | 2.33 | 6 | 2 | 2 | 1 |
Other divisor rules are possible, including Modified Saint-Laguë (1.4, 3, 5, 7, 9, etc):
| Quotients | Seats | ||||||
| 42.14 | 18.57 | 11.43 | 5 | 1 | 0 | 0 | 0 |
| 19.67 | 18.57 | 11.43 | 5 | 2 | 0 | 0 | 0 |
| 11.80 | 18.57 | 11.43 | 5 | 2 | 1 | 0 | 0 |
| 11.80 | 8.67 | 11.43 | 5 | 3 | 1 | 0 | 0 |
| 8.43 | 8.67 | 11.43 | 5 | 3 | 1 | 1 | 0 |
| 8.43 | 8.67 | 5.33 | 5 | 3 | 2 | 1 | 0 |
| 8.43 | 5.20 | 5.33 | 5 | 4 | 2 | 1 | 0 |
| 6.56 | 5.20 | 5.33 | 5 | 5 | 2 | 1 | 0 |
| 5.36 | 5.20 | 5.33 | 5 | 6 | 2 | 1 | 0 |
| 4.54 | 5.20 | 5.33 | 5 | 6 | 2 | 2 | 0 |
| 4.54 | 5.20 | 3.20 | 5 | 6 | 3 | 2 | 0 |
Danish (1, 4, 7, 10, 13, etc):
| Quotients | Seats | ||||||
| 59 | 26 | 16 | 7 | 1 | 0 | 0 | 0 |
| 14.75 | 26 | 16 | 7 | 1 | 1 | 0 | 0 |
| 14.75 | 6.50 | 16 | 7 | 1 | 1 | 1 | 0 |
| 14.75 | 6.50 | 4 | 7 | 2 | 1 | 1 | 0 |
| 8.43 | 6.50 | 4 | 7 | 3 | 1 | 1 | 0 |
| 5.90 | 6.50 | 4 | 7 | 3 | 1 | 1 | 1 |
| 5.90 | 6.50 | 4 | 1.75 | 3 | 2 | 1 | 1 |
| 5.90 | 3.71 | 4 | 1.75 | 4 | 2 | 1 | 1 |
| 4.54 | 3.71 | 4 | 1.75 | 5 | 2 | 1 | 1 |
| 3.69 | 3.71 | 4 | 1.75 | 5 | 2 | 2 | 1 |
| 3.69 | 3.71 | 2.29 | 1.75 | 5 | 3 | 2 | 1 |
and Imperiali (1, 1.5, 2, 2.5, 3, 3.5, etc):
| Quotients | Seats | ||||||
| 59 | 26 | 16 | 7 | 1 | 0 | 0 | 0 |
| 39.33 | 26 | 16 | 7 | 2 | 0 | 0 | 0 |
| 29.50 | 26 | 16 | 7 | 3 | 0 | 0 | 0 |
| 23.60 | 26 | 16 | 7 | 3 | 1 | 0 | 0 |
| 23.60 | 17.33 | 16 | 7 | 4 | 1 | 0 | 0 |
| 19.67 | 17.33 | 16 | 7 | 5 | 1 | 0 | 0 |
| 16.86 | 17.33 | 16 | 7 | 5 | 2 | 0 | 0 |
| 16.86 | 13 | 16 | 7 | 6 | 2 | 0 | 0 |
| 14.75 | 13 | 16 | 7 | 6 | 2 | 1 | 0 |
| 14.75 | 13 | 10.67 | 7 | 7 | 2 | 1 | 0 |
| 13.11 | 13 | 10.67 | 7 | 8 | 2 | 1 | 0 |
So, let us bring all these examples together showing the order in which seats were allocated for the quotient methods:
Method |
Target proportions |
Seat total |
l |
Working |
Seats |
|||||||||
| Imperiali | 59 | 26 | 16 | 7 | 11 | A A A B A A B A C A A | 8 | 2 | 1 | 0 | ||||
| d’Hondt / Jefferson | 59/7 | A A B A C A B A A B A | 7 | 3 | 1 | 0 | ||||||||
| Modified Saint-Laguë | A A B A C B A A A C B | 6 | 3 | 2 | 0 | |||||||||
| L. R. / Hamilton | 6.009 | 2.648 | 1.630 | 0.713 | 6 | 3 | 1 | 1 | ||||||
| Saint-Laguë / Webster | 32/3 | A B A C A B A D A A C | 6 | 2 | 2 | 1 | ||||||||
| Danish | A B C A A D B A A C B | 5 | 3 | 2 | 1 | |||||||||
It can be seen immediately that Imperiali is the most favourable to large parties. Imperiali has slowly-increasing divisors (1, 1.5, 2, 2.5, ...); large parties gain many seats before their quotients are reduced below those of the smaller parties. In contrast, the Danish divisors (1, 4, 7, 10, ...) increase so fast that large parties are quickly cut down — much to the benefit of smaller parties.
In the 59:26:16:7 example, the quota (unrounded) seat allocations were 6.009, 2.648, 1.630 and 0.713. In this example only two of the above systems ‘breached quota’, that is, gave a seat allocation smaller than rounded-down quota or larger than this plus 1. However, any of these systems other than Hamilton / Largest Remainder can breach quota, as evidenced in the following table:
Method |
Target proportions |
Seat total |
Quota |
Seats |
|||||||||
| Imperiali | 3 | 1 | 1 | 3 | 1.8 | 0.6 | 0.6 | 3 | 0 | 0 | |||
| d’Hondt / Jefferson | 5 | 1 | 1 | 4 | 2.857 | 0.571 | 0.571 | 4 | 0 | 0 | |||
| Modified Saint-Laguë | 7 | 1 | 1 | 5 | 3.889 | 0.556 | 0.556 | 5 | 0 | 0 | |||
| Saint-Laguë / Webster | 14 | 3 | 1 | 1 | 8 | 5.895 | 1.263 | 0.421 | 0.421 | 7 | 1 | 0 | 0 |
| Danish | 9 | 1 | 1 | 5 | 4.091 | 0.455 | 0.455 | 3 | 1 | 1 | |||
There are two frequently seen contexts in which seats have to be assigned proportional to some number. The first context, in which we are interested here, is following an election. The second is the assignment of seats to a geographical region. The difference is that, usually, it is required that every region has at least one seat, however small. Applying such a system to post-election assignments would ensure that every party gets a seat.
An example is the ‘Adams method’ of apportionment, which is similar to the Webster and Jefferson methods, except that the number of seats is rounded up. Another, the ‘method of equal proportions’, again uses a divisor, but rounds up only if the number of seats to be allocated exceeds the geometric average of itself rounded down and itself plus 1 rounded down.
Because the US constitution says merely that the House of Representatives “shall be apportioned among the several States according to their respective numbers”, and that “each State shall have at least one Representative”, these systems have been of interest to the US courts. An explanation of the 1991 and 1992 cases challenging the use of the method of equal proportions can be found here.
In order to acquire a better feel for the properties of the six systems under review, a simple statistical analysis has been performed. We have considered a 6-party election, in which seats are to be proportional to votes. The relative sizes of the votes of the parties are constrained, so the number of votes received by the i’th largest party, divided by the number of votes received by the i+1’th largest party, is in the range 3^½ to 2^¼. In other words, each party is between 18.92% and 73.2% larger than the next-largest party. We then ignore any vote distribution that causes any of the 6 electoral systems under review to have a draw.
For 11 seats we consider the 82,837,504 vote distributions running from 8:6:5:4:3:2 to 152:108:78:63:44:33. For each vote distribution we calculate the average number of seats won by the largest party, by the second-largest, the third-largest, etc. For each of the six methods under consideration, we observe the difference between that method and the average. We calculate both an average difference, and the standard deviation of that difference. The following charts show the average differences, and their standard deviation.
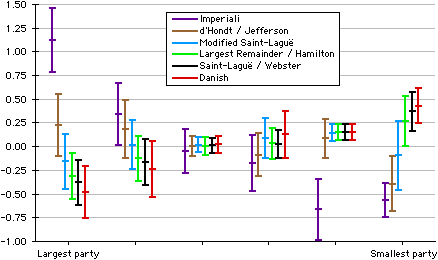
It is immediately apparent that Imperiali greatly favours the larger parties. Indeed, on average the largest party does 0.9 seats better under Imperiali than under d’Hondt / Jefferson. Jefferson also favours larger parties, though much less than Imperiali. For the middle two parties Jefferson is more consistent than Imperiali, as measured by its standard deviation from its average behaviour. In this model Modified Saint-Laguë most favours the fourth largest party, though is the most random in its treatment of the smallest party. Largest Remainder / Hamilton and Saint-Laguë / Webster are very similar, with the former being 0.06 seats more generous to the largest party, and 0.1 seats less to the smallest. The standard deviations of their differences from the average are also close. Danish favours small parties, though by less, and less randomly, than Imperiali favours the large.
A similar pattern occurs with a 659-seat constituency:
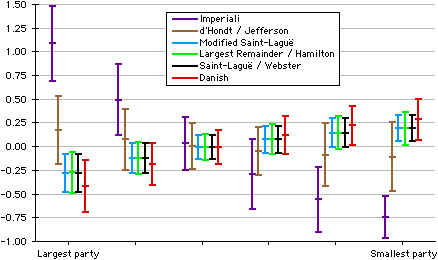
except that Modified Saint-Laguë, Largest Remainder / Hamilton and Saint-Laguë / Webster are so close as to be almost indistinguishable, with Hamilton being (by an edge) the most random.
Quota breaches can also be addressed statistically. The following table shows the average size of breaches of upper quota (top item in each cell), and of lower quota (lower item). A blank indicates that no breaches were observed; therefore ‘0.00’ indicates that they were present but rare. Imperiali frequently breaches upper quota for the large parties, and lower quota for the small. Jefferson also over-helps the largest party, though less than Imperiali. Largest Remainder never breaches quota (by construction), the others do so, but rarely.
| Quota breaches with 659 seats | Average extent of breaches of upper quota Average extent of breaches of lower quota | |||||
| Party size: | Largest | Smallest | ||||
| Danish | -0.00 | -0.00 | | | | |
| Saint-Laguë / Webster | 0.00 -0.00 | | | | | |
| Largest Remainder / Hamilton | | | | | | |
| Modified Saint-Laguë | 0.00 -0.00 | | | | | |
| d’Hondt / Jefferson | 0.06 | 0.00 | | | | |
| Imperiali | 0.87 | 0.14 | 0.00 | -0.01 | -0.21 | -0.45 |
So what does all this imply for PR-Squared?
Julian D. A. Wiseman, July 2001
| Main index | Top | About author |